Objectif : Tracer la caractéristique U = f(I) d’une photorésistance (LDR) en faisant varier une tension aux bornes d’une association série LDR-résistance R connue (par exemple 1kΩ).
Pour cela, on peut réaliser un montage électrique classique et mesurer les valeurs de I (avec un ampèremètre/ ou voltmètre aux bornes de R) et U aux bornes de la photorésistance (avec un voltmètre) en utilisant une alimentation variable.
On pourrait réaliser des mesures pour 3 éclairements différents.
Schéma du montage (pont diviseur de tension) :
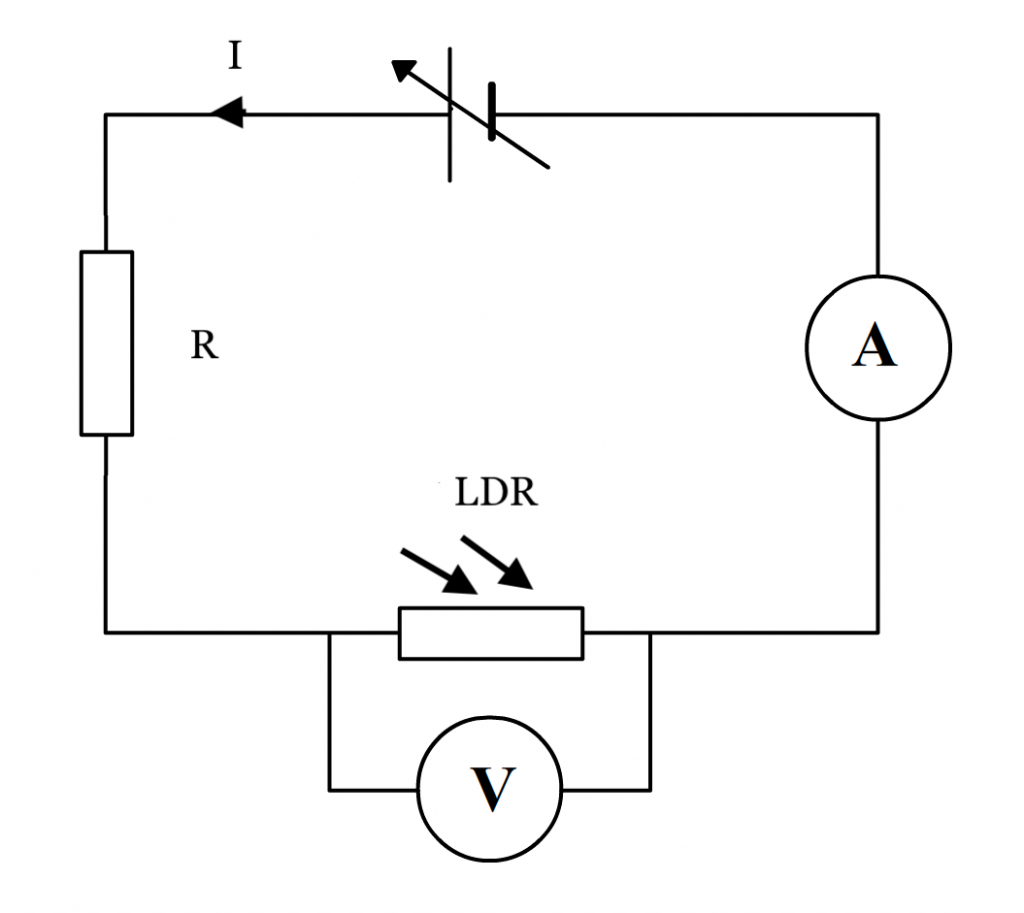
Bonus : Faire une régression linéaire en utilisant le module linregress (en important le module stats de scipy).
On utilise le programme Python Tracé caracteristique U=f(I) avec regression lineaire en inscrivant dans des listes les valeurs mesurées .
# -*- coding: utf-8 -*-
"""
Programme Python pour tracé caractéristique d'une photorésistance (ou autre capteur résistif).
Une tension variable est appliquée aux bornes d’une association série LDR-résistance R connue (par exemple 1kΩ).
On mesure la tension aux bornes de la photorésistance avec un voltmètre et l'intensité parcourant le circuit I soit avec un voltmetreaux bornes de la résistance R (I = Ur/R).
Puis il faut créer des « listes » dans lesquelles on inscrit les valeurs en abscisses et en ordonnées des points du graphique que l'on souhaite tracer.
"""
######################################### IMPORTATION DES BIBLIOTHEQUES ET MODULES ########################################################
import numpy as np # numpy pour les maths , par exemple pour créer 256 valeurs régulièrement espacées entre 0 et 10 : np.linspace(0,10,256)
import matplotlib.pyplot as plt # pour les graphiques
from scipy import stats # module permettant de faire la régression linéaire à partir d'une liste X et d'une liste Y, stats.linregress(X,Y) renvoie 5 valeurs. Les 3 premières valeurs sont la pente, l'ordonnée à l'origine, et le coefficient de corrélation (à mettre au carré)
######################################### Valeurs de I et de U pour différents éclairements de la photorésistance #######################################################
I=[0,0.04,0.08,0.14,0.18,0.25] #créer la liste des valeurs des intensités en abscisses
U1=[0,1,2,3,4,5] #créer liste des valeurs des tensions en ordonnées
U2=[0,2,4,6,8,10]
U3=[0,4,8,12,16,20]
################################# REGRESSION LINEAIRE ET TRACE DE GRAPHIQUE ########################################################################################
eq1 = stats.linregress (I,U1) # pour faire la régression linéaire sur la courbe 1
pente1 = eq1[0] # pente
ordorig1 = eq1[1] # ordonnée à l'origine
coeff1_carre = eq1[2]**2 # coefficient de corrélation au carré r²
eq2 = stats.linregress (I,U2) # pour faire la régression linéaire sur la courbe 2
pente2 = eq2[0] # pente
ordorig2 = eq2[1] # ordonnée à l'origine
coeff2_carre = eq2[2]**2 # coefficient de corrélation au carré r²
eq3 = stats.linregress (I,U3) # pour faire la régression linéaire sur la courbe 3
pente3 = eq3[0] # pente
ordorig3 = eq3[1] # ordonnée à l'origine
coeff3_carre = eq3[2]**2 # coefficient de corrélation au carré r²
Xcalc = np.linspace(0,max(I) , 256) # création de points pour le tracé du modèle : on crée 256 points régulièrement espacés entre 0 et la valeur max de I
Y1calc = pente1*Xcalc+ordorig1 # on fait calculer U1 avec les paramètres de la régression linéaire pour ces valeurs de I
texte1 = 'Eclairement 1 U1 = '+str(round(pente1,3))+' I + '+str(round(ordorig1,3))+' R² = '+str(round(coeff1_carre,3)) # on affiche l'équation de la droite avec 3 décimales
print (texte1)
Y2calc = pente2*Xcalc+ordorig2 # on fait calculer U2 avec les paramètres de la régression linéaire pour ces valeurs de I
texte2 = 'Eclairement 2 U2 = '+str(round(pente2,3))+' I + '+str(round(ordorig2,3))+' R² = '+str(round(coeff2_carre,3)) # on affiche l'équation de la droite avec 3 décimales
print (texte2)
Y3calc = pente3*Xcalc+ordorig3 # on fait calculer U3 avec les paramètres de la régression linéaire pour ces valeurs de I
texte3 = 'Eclairement 3 U3 = '+str(round(pente3,3))+' I + '+str(round(ordorig3,3))+' R² = '+str(round(coeff3_carre,3)) # on affiche l'équation de la droite avec 3 décimales
print (texte3)
plt.title("Caractéristique de la photorésistance:U=f(I) pour 3 éclairements") # mettre un titre au graphique
plt.scatter(I,U1, color ='r', marker = 'o') # On affiche les points de coordonnées (I,U1) avec des points rouges
plt.plot(Xcalc,Y1calc,color = 'b',label = texte1) # Affichage de la courbe modélisée en bleu
plt.scatter(I,U2, color ='r', marker = '+') # On affiche les points de coordonnées (I,U2) avec des croix rouges
plt.plot(Xcalc,Y2calc,color = 'g',label = texte2) # Affichage de la courbe modélisée en vert
plt.scatter(I,U3, color ='r', marker = 'x') # On affiche les points de coordonnées (I,U3) avec des croix rouges
plt.plot(Xcalc,Y3calc,color = 'r',label = texte3) # Affichage de la courbe modélisée en rouge
plt.xlabel("intensité en A") #nommer l'axe des abscisses
plt.ylabel("tension U en V") #nommer l'axe des ordonnées
plt.legend() # pour afficher les légendes (label)
plt.show() #afficher le graphique (ne rien mettre dans la parenthèse)