Merci à l’auteur de cet article qui a été une ressource très précieuse pour la réalisation de cette activité :
Objectifs et enjeux
Dans le cadre des nouveaux programmes CPGE, nous avons recherché un moyen de réaliser des acquisitions d’oscillations forcées avec un accéléromètre et un microcontrôleur. Nous souhaitons réaliser un graphe en temps réel et modéliser la courbe pour mesurer l’amplitude et la fréquence des oscillations.
Accéléromètre et carte Arduino
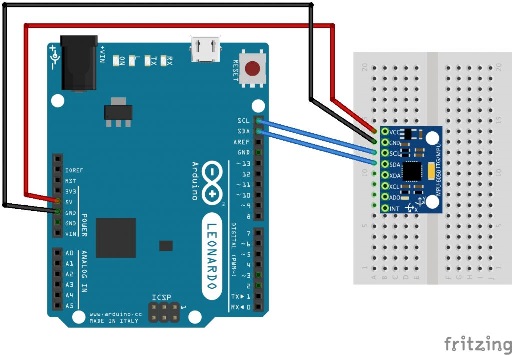
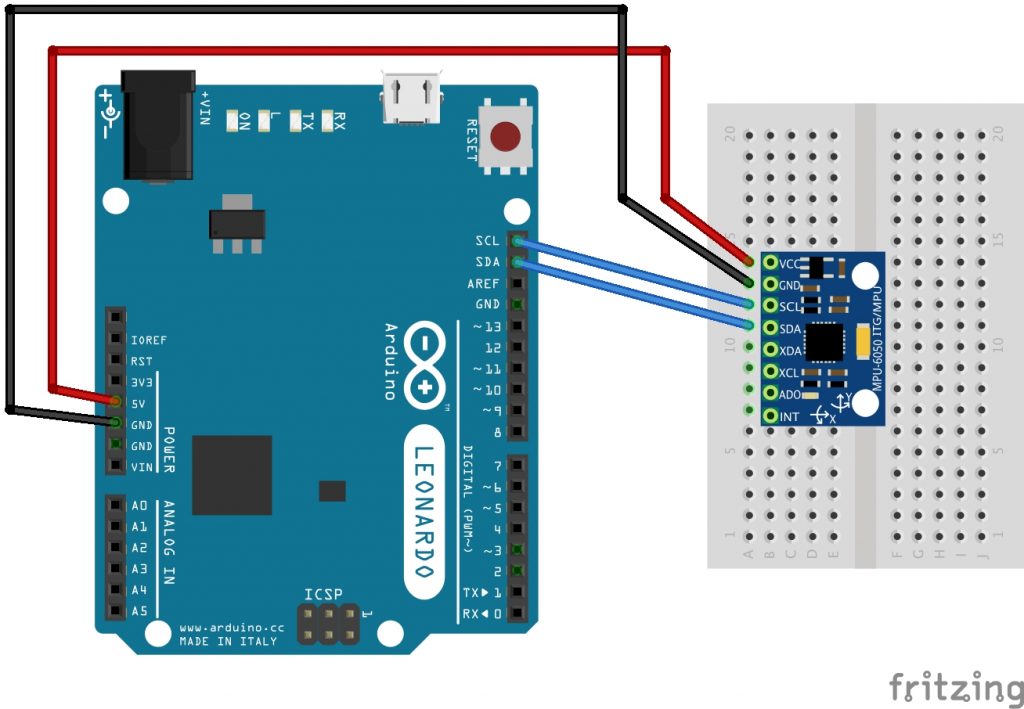
L’accéléromètre-gyroscope utilisé ici est le MPU 6050.
Les branchements sont relativement simples car il suffit de brancher les bornes Vcc, GND, SCL et SDA pour récupérer les 3 composantes de l’accélération et les 3 composantes de l’angle de rotation.
Il est nécessaire d’installer préalablement les bibliothèques I2C et MPU6050 développées par Jeff Rowberg du MIT :
Pour installer ces biblothèques :
- Ouvrir le logiciel Arduino
- À partir du menu [Croquis][Inclure une librairie][Ajouter la librairie .ZIP], installer la librairie « I2dev.zip» (disponible sur ce lien : I2dev.zip)
- À partir du menu [Croquis][Inclure une librairie][Ajouter la librairie .ZIP], installer la librairie « MPU6050.zip» (disponible sur ce lien : MPU6050.zip)
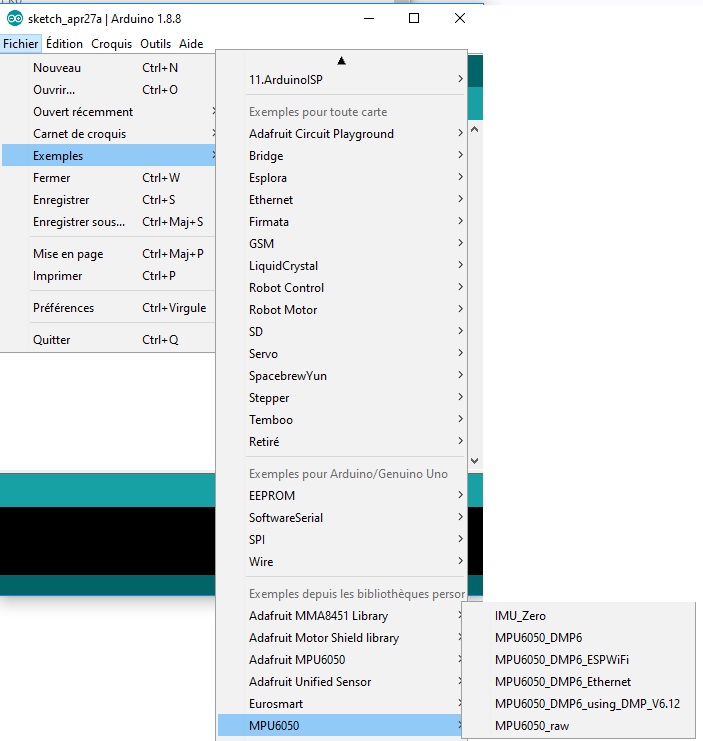
Étalonnage de l’accéléromètre
Pour étalonner l’accéléromètre, téléverser le programme IMU_Zero à partir du menu [Fichier]Exemples][MPU6050]. On laissera l’accéléromètre au repos et à plat.
Ouvrir le moniteur série, puis attendre la fin de l’étalonnage (l’opération prend quelques minutes)
Dispositif expérimental pour l’acquisition
Nous utilisons un vibreur de Melde alimenté par un GBF (modèle avec lequel il est possible de régler précisément la fréquence).
Il faudra utiliser un suiveur de puissance type Geneboost entre le GBF et le vibreur pour éviter les chutes de tension.
Matériel utilisé :
- GBF Centrad GF265
- Geneboost Pierron
- Un ressort de 20 N/m coupé en deux (donc deux ressorts de 40 N/m !)
- Accéléromètre MPU6050 fixé sur pièce imprimée en 3D qui contient une masse de 20 g.
- Support imprimé en 3D sur masse de 500 g
Les fichiers STL des pièces 3D sont disponibles ici.
Téléversement du programme Arduino
Le programme téléversé dans la carte Arduino est le suivant, il est librement inspiré du programme de l’article disponible à cette adresse : http://gilles.thebault.free.fr/spip.php?article32
Certaines lignes ont été désactivées (transformées en commentaires avec \\) pour ne garder que les valeurs des 3 composantes de l’accélération
#include "Wire.h" // Arduino Wire library
#include "I2Cdev.h" //bibliothèque I2Cdev à installer
#include "MPU6050.h" //bibliothèque MPU6050 à installer
// AD0 low = 0x68 (default for InvenSense evaluation board)
// AD0 high = 0x69
MPU6050 accelgyro;
long temps;
int16_t ax, ay, az; //mesures brutes
int16_t gx, gy, gz;
void setup() {
Wire.begin(); // bus I2C
Serial.begin(9600); // liaison série
while (!Serial) {
; // wait for serial port to connect. Needed for native USB (LEONARDO)
}
accelgyro.initialize(); // initialize device
temps = millis();
}
void loop() {
// accelgyro.getMotion6(&ax, &ay, &az, &gx, &gy, &gz);
temps = millis();
// On peut aussi utiliser ces méthodes
accelgyro.getAcceleration(&ax, &ay, &az);
//accelgyro.getRotation(&gx, &gy, &gz);
// Affichage accel/gyro x/y/z
// Serial.print("a/g:\t");
// Serial.print(ax);
// Serial.print("\t");
Serial.print("t : ");
Serial.print("\t");
Serial.print(temps);
Serial.print("\t");
Serial.print("ax : ");
Serial.print("\t");
Serial.print(ax);//
Serial.print("\t");
Serial.print("ay : ");
Serial.print("\t");
Serial.print(ay);//
Serial.print("\t");
Serial.print("az : ");
Serial.print("\t");
Serial.print(az);
Serial.println("\t");
// Serial.print(gx);
// Serial.print("\t");
// Serial.print(gy);
// Serial.print("\t");
// Serial.print(gz);
// Serial.println("\t");
delay(10);
}
Récupération des données avec Python
Une fois ce code Arduino téléversé, nous pouvons récupérer les valeurs avec Python (par biais d’un IDE comme Pyzo, Spyder, IDLE, Sublime Text,..). Il est alors possible de tracer un graphe en temps réel, traiter les données, modéliser les courbes etc…
Dans cet article , je ne rentrerai pas dans les détails pour les étapes de récupération de données. pour cela, je vous invite à consulter l’article qui explique les différentes étapes sur ce lien :
Récupération des données d’une carte Arduino avec Python
Voici le script Python à exécuter :
#importation des modules
import serial
import serial.tools.list_ports # pour la communication avec le port série
import matplotlib.pyplot as plt # pour le tracé de graphe
from matplotlib import animation # pour la figure animée
import time # gestion du temps
import numpy as np # numpy pour l'importation des donnees en format txt
from scipy.optimize import curve_fit
liste_a = [] # liste pour stocker les valeurs de distance
liste_t = []
t_acquisition = 10.0 # en s
amax =2 # en g
amin= 0 # en g
dt=0.1
#pour le graphe en teamax= 3 # en temps réel
def animate(i):
line1 = Data.readline()
print (line1)
# on retire les caractères d'espacement en début et fin de chaîne
listeDonnees = line1.strip()
# on sépare les informations reçues séparées par les espaces et on stocke ces informations dans une liste pour chacune de lignes
listeDonnees = line1.split()
print (listeDonnees)
if len(listeDonnees) == 12 : # parfois des lignes de données vides peuvent être envoyées, il faut les "écarter"
accelx = (float(listeDonnees[5].decode()))/16834 # après consulation des données, nous choisissons le 6 ème élément de listeDonnees, on convertit l'accélération en g
accely = (float(listeDonnees[8].decode()))/16834 # après consulation des données, nous choisissons le 6 ème élément de listeDonnees, on convertit l'accélération en g
accelz = (float(listeDonnees[11].decode()))/16834 # après consulation des données, nous choisissons le 6 ème élément de listeDonnees, on convertit l'accélération en g
accel =np.sqrt(accelx**2+accely**2 +accelz**2)
temps = (float(listeDonnees[2].decode()))/1000.0 # après consulation des données, nous choisissons le 1er élément de listeDonnees
while temps <= t_acquisition:
liste_a.append(accel)
print("a = %f"%(accel), " g") # affichage de la valeur de la distance
liste_t.append(temps)
print("temps = %f"%(temps), " s") # affichage de la valeur du temps en partant de 0
line.set_data(liste_t,liste_a)
return line,
# Fonction pour la récupération des données série venant de la carte Arduino
def recup_port_Arduino() :
ports = list(serial.tools.list_ports.comports())
for p in ports:
if 'Arduino' in p.description :
mData = serial.Serial(p.device,9600)
print(mData.is_open) # Affiche et vérifie que le port est ouvert
print(mData.name) # Affiche le nom du port
return mData
Data =recup_port_Arduino() #récupération des données
# Création figure
fig=plt.figure()
line, = plt.plot([],[])
plt.xlim(0, t_acquisition)
plt.ylim(amin,amax)
plt.xlabel('temps en s')
plt.ylabel('a en g')
plt.grid()
#Animation
ani = animation.FuncAnimation(fig, animate, frames=2000, interval=20,repeat=False)
plt.show()
plt.close(fig)
Data.close()
#Ecriture dans un fichier txt
lines=['t\ta\n'] #première ligne du fichier txt
for i in range (len (liste_a)):
line = str(liste_t[i]) +'\t'+ str(liste_a[i])+'\n'
lines.append(line)
fichier = open('data_accelerometre.txt', 'w').writelines(lines) #création d'un nouveau fichier texte
t = np.array(liste_t)
acc = np.array(liste_a)
# Fonction d'estimation de la fréquence
def estim_freq(y) :
compt = 0
moy = np.mean(y)
etat_old = False
etat_new = False
for i in range (len(y)) :
if y[i] < moy :
etat_new = True
else :
etat_new = False
if etat_old != etat_new :
etat_old = etat_new
compt += 1
return (compt/(2*t_acquisition))
# Fonction d'estimation des valeurs des paramètres de la modélisation
def get_p0(x, y):
A0 = (np.max(y)-np.min(y))/2
f0 =estim_freq(y)
phase0 =0
offset0 = np.mean(y)
return [A0, f0, phase0,offset0]
def f(x,a,b,c,d):
return (a*np.sin(2.*np.pi*b*x+c)+d)
popt,pcov = curve_fit (f,t,acc,p0=get_p0(t,acc))
# popt,pcov = curve_fit (f,t,acc)
texte = 'Accélération = '+str(round(float(popt[0]),2))+' sin (2pi*'+str(round(float(popt[1]),2))+'*t+'+str(round(float(popt[2]),2))+') + '+str(round(float(popt[3]),2))+'\n' +'A = '+str(round(float(popt[0]),2))+'; f = '+str(round(float(popt[1]),2))+' ; phase ='+str(round(float(popt[2]),2))+' ; offset = '+str(round(float(popt[3]),2))
# afficher points avec croix rouges. Inserer texte (titre, nom des axes,…)
plt.figure()
plt.scatter(t, acc, c = 'red', marker = '+')
plt.plot(t,f(t,*popt),'g--',label = texte)
plt.xlabel("t en s")
plt.ylabel("a en g")
plt.legend() # pour afficher les légendes (label)
plt.show()
print (texte)
Quelques précisions concernant la modélisation : la fonction CURVE FIT de scipy
Les lignes de code concernant la modélisation mérite des éclaircissements !
Nous utilisons la fonction curve_fit de scipy (en l’important avec
from scipy.optimize import curve_fitNous définissons une fonction pour le modèle à trouver :
def f(x,a,b,c,d):
return (a*np.sin(2.*np.pi*b*x+c)+d)Pour ajuster la courbe par rapport au modèle, il faut écrire :
popt,pcov = curve_fit (f,t,acc)Seul popt nous intéresse, il s’agit des paramètres d’optimisation de la courbe par rapport au modèle (c’est à dire ici ces 4 valeurs: amplitude (a), fréquence(b), phase(c), offset(d) )
Même si pcov ne nous intéresse pas,nous sommes obligés d’écrire popt,pcov !
… malheureusement cela ne suffit pas 🙁 Il faut « aider » le programme en donnant une estimation de ces paramètres pour que l’optimisation se fasse correctement.
Pour cela il faut définir au préalable une fonction get_p0(x,y) pour estimer ces valeurs :
- Pour l’amplitude, on divise par deux l’écart entre la valeur minimale et la valeur maximale des accélérations mesurées
- Par défaut, on définit la phase égale à 0
- Pour la tension de décalage (ou offset), on calcule la moyenne des valeurs d’accélération mesurées
def get_p0(x, y):
A0 = (np.max(y)-np.min(y))/2
f0 =estim_freq(y)
phase0 =0
offset0 = np.mean(y)Et pour l’estimation de la fréquence ?
On définit (encore !) une petite fonction qui va compter les passages par la valeur moyenne (donc toutes les demi-périodes). Cette fonction va retourner la valeur nombre de comptages/temps d’acquisition … qu’il faut diviser par deux pour une période entière !
Voici cette fonction (qu’il faut définir avant get_p0) :
def estim_freq(y) :
compt = 0
moy = np.mean(y)
etat_old = False
etat_new = False
for i in range (len(y)) :
if y[i] < moy :
etat_new = True
else :
etat_new = False
if etat_old != etat_new :
etat_old = etat_new
compt +=
return (compt/(2*t_acquisition))En petit bonus, un script Python permettant de faire la modélisation directement à partir de la dernière acquisition (sans recommencer l’acquisition) à partir des valeurs sauvegardées dans un fichier txt :
import matplotlib.pyplot as plt # pour les graphiques
import numpy as np # numpy pour l'importation des donnees en format txt
from scipy.optimize import curve_fit
importation des donnees txt obtenues apres pointage en supprimant la premiere ligne dans le fichier texte
lines = open('data_accelerometre.txt').readlines() #on lit les lignes du fichier texte
open('data_new.txt', 'w').writelines(lines[1:]) #création d'un nouveau fichier texte sans la première ligne
data = np.loadtxt('data_new.txt')# importation du nouveau fichier texte pour récupérer les valeurs det, x et y dans un tableau
t = data[:,0] # selection de la premiere colonne
acc = data[:,1] # selection de la deuxieme colonne
def estim_freq(y) :
compt = 0
moy = np.mean(y)
etat_old = False
etat_new = False
for i in range (len(y)) :
if y[i] < moy :
etat_new = True
else :
etat_new = False
if etat_old != etat_new :
etat_old = etat_new
compt += 1
return (compt/(2*10.0)) #temps d'acquisition de 10s
Fonction d'estimation des valeurs des paramètres de la modélisation
def get_p0(x, y):
A0 = (np.max(y)-np.min(y))/2 f0 =estim_freq(y) phase0 =0 offset0 = np.mean(y) return [A0, f0, phase0,offset0]
def f(x,a,b,c,d):
return (anp.sin(2.np.pibx+c)+d)
pop,pcov = curve_fit (f,t,acc)
popt,pcov = curve_fit (f,t,acc,p0=get_p0(t,acc))
texte = 'Accélération = '+str(round(float(popt[0]),2))+' sin (2pi'+str(round(float(popt[1]),2))+'t+'+str(round(float(popt[2]),2))+') + '+str(round(float(popt[3]),2))+'\n' +'A = '+str(round(float(popt[0]),2))+'; f = '+str(round(float(popt[1]),2))+' ; phase ='+str(round(float(popt[2]),2))+' ; offset = '+str(round(float(popt[3]),2))
afficher points avec croix rouges. Inserer texte (titre, nom des axes,…)
plt.figure(1)
plt.plot(t, acc, c = 'red', marker = '+')
plt.plot(t,f(t,*popt),'g--',label = texte)
plt.xlabel("t en s")
plt.ylabel("a en g")
plt.legend() # pour afficher les légendes (label)
plt.show()
print (texte)
print(get_p0(t,acc))
estim_freq(acc)Changer de gamme pour de plus grandes accélérations
En cas d’expériences avec des mouvements rapdes comme pour des chocs, il est nécessaire de mesurer des valeurs d’accélération plus élevées.
Pour travailler sur une gamme -16g/+16g (au lieu de -2g/+2g), il suffit de rajouter une ligne de code dans le setup du programme Arduino :
accelgyro.setFullScaleAccelRange(3); // pour la gamme -16g/+16gVoici le code Arduino modifié à téléverser (avec mesure de ax seulement):
#include "Wire.h" // Arduino Wire library
#include "I2Cdev.h" //bibliothèque I2Cdev à installer
#include "MPU6050.h" //bibliothèque MPU6050 à installer
// AD0 low = 0x68 (default for InvenSense evaluation board)
// AD0 high = 0x69
MPU6050 accelgyro;
long temps;
int16_t ax, ay, az; //mesures brutes
int16_t gx, gy, gz;
void setup() {
Wire.begin(); // bus I2C
Serial.begin(9600); // liaison série
while (!Serial) {
; // wait for serial port to connect. Needed for native USB (LEONARDO)
}
accelgyro.initialize(); // initialize device
accelgyro.setFullScaleAccelRange(3); // pour la gamme -16g/+16g
temps = millis();
}
void loop() {
temps = millis();
accelgyro.getMotion6(&ax, &ay, &az, &gx, &gy, &gz);
Serial.print(temps);
Serial.print("\t");
Serial.println(ax);
}Si on fait cette modification, nous allons récupérer 2^16 valeurs comprises entre -16g et 16g donc 1g correspond à 2048 (au lieu de 16384) .
Ci-dessous le script Python pour récupérer les données :
#importation des modules
import serial
import serial.tools.list_ports # pour la communication avec le port série
import matplotlib.pyplot as plt # pour le tracé de graphe
from matplotlib import animation # pour la figure animée
# import time # gestion du temps
import numpy as np # numpy pour l'importation des donnees en format txt
from scipy.optimize import curve_fit
liste_a = [] # liste pour stocker les valeurs de distance
liste_t = []
t_acquisition = 10.0 # en s
amax =4 # en g
amin= -4 # en g
# dt=0.1
#pour le graphe en temps réel
def animate(i):
line1 = Data.readline()
print (line1)
# on retire les caractères d'espacement en début et fin de chaîne
listeDonnees = line1.strip()
# on sépare les informations reçues séparées par les espaces et on stocke ces informations dans une liste pour chacune de lignes
listeDonnees = line1.split()
print (listeDonnees)
if len(listeDonnees) == 2 : # parfois des lignes de données vides peuvent être envoyées, il faut les "écarter"
accel = (float(listeDonnees[1].decode()))/2048.0 # après consulation des données, nous choisissons le 6 ème élément de listeDonnees, on convertit l'accélération en g
temps = (float(listeDonnees[0].decode()))/1000.0 # après consulation des données, nous choisissons le 1er élément de listeDonnees
while temps <= t_acquisition:
liste_a.append(accel)
print("a = %f"%(accel), " g") # affichage de la valeur de la distance
liste_t.append(temps)
print("temps = %f"%(temps), " s") # affichage de la valeur du temps en partant de 0
line.set_data(liste_t,liste_a)
return line,
# Fonction pour la récupération des données série venant de la carte Arduino
def recup_port_Arduino() :
ports = list(serial.tools.list_ports.comports())
for p in ports:
if 'Arduino' in p.description :
mData = serial.Serial(p.device,9600)
print(mData.is_open) # Affiche et vérifie que le port est ouvert
print(mData.name) # Affiche le nom du port
return mData
Data =recup_port_Arduino() #récupération des données
# Création figure
fig=plt.figure()
line, = plt.plot([],[])
plt.xlim(0, t_acquisition)
plt.ylim(amin,amax)
plt.xlabel('temps en s')
plt.ylabel('a en g')
plt.grid()
#Animation
ani = animation.FuncAnimation(fig, animate, frames=2000, interval=20,repeat=False)
plt.show()
plt.close(fig)
Data.close()
#Ecriture dans un fichier txt
lines=['t\ta\n'] #première ligne du fichier txt
for i in range (len (liste_a)):
line = str(liste_t[i]) +'\t'+ str(liste_a[i])+'\n'
lines.append(line)
fichier = open('data_accelerometre.txt', 'w').writelines(lines) #création d'un nouveau fichier texte
t = np.array(liste_t)
acc0 = np.array(liste_a)
acc_moy=np.mean(acc0)
acc = acc0-acc_moy
def estim_freq(y) :
compt = 0
moy = np.mean(y)
etat_old = False
etat_new = False
for i in range (len(y)) :
if y[i] < moy :
etat_new = True
else :
etat_new = False
if etat_old != etat_new :
etat_old = etat_new
compt += 1
return (compt/(2*t_acquisition))
def get_p0(x, y):
A0 = (np.max(y)-np.min(y))/2
f0 =estim_freq(y)
phase0 =0
offset0 = np.mean(y)
return [A0, f0, phase0,offset0]
def f(x,a,b,c,d):
return (a*np.sin(2.*np.pi*b*x+c)+d)
Xcalc = np.linspace(0,max(t) , 1024) # création de points pour le tracé du modèle : on crée 1024 points régulièrement espacés entre 0 et la valeur max de I
pop,pcov = curve_fit (f,t,acc,p0=get_p0(t,acc))
# pop,pcov = curve_fit (f,t,acc)
texte = 'Accélération = '+str(round(float(pop[0]),2))+' sin (2pi*'+str(round(float(pop[1]),2))+'*t+'+str(round(float(pop[2]),2))+') + '+str(round(float(pop[3]),2))+'\n' +'A = '+str(round(float(pop[0]),2))+'; f = '+str(round(float(pop[1]),2))+' ; phase ='+str(round(float(pop[2]),2))+' ; offset = '+str(round(float(pop[3]),2))
# afficher points avec croix rouges. Inserer texte (titre, nom des axes,…)
plt.figure()
plt.scatter(t, acc, c = 'red', marker = '+')
plt.plot(Xcalc,f(Xcalc,*pop),'g--',label = texte)
plt.xlabel("t en s")
plt.ylabel("a en g")
plt.legend() # pour afficher les légendes (label)
plt.show()
print (texte)